It is required to obtain the Y-Matrix for the following network.

4 Ω 1 1 Ω 2 j1 Ω 3 4 3 Ω -j4 Ω 2 Ω -j2 Ω j3 Ω
4 Ω 1 1 Ω 2 j1 Ω 3 4 3 Ω -j4 Ω 2 Ω -j2 Ω j3 Ω

This network has four nodes numbered 1, 2, 3, and 4.

4 Ω 1 1 Ω 2 j1 Ω 3 4 3 Ω -j4 Ω 2 Ω -j2 Ω j3 Ω

The impedances of the branches are shown, for example, the impedance of the branch between nodes 2 and 4 is 4 ohms.

4 Ω 1 1 Ω 2 j1 Ω 3 4 3 Ω -j4 Ω 2 Ω -j2 Ω j3 Ω

To obtain the Y-Matrix for the following network, you must first calculate the admittances of the branches. For example, the admittance corresponding to the branch between nodes 3 and 4 is

4 Ω 1 1 Ω 2 j1 Ω 3 4 3 Ω j0.25 ℧ 2 Ω -j2 Ω j3 Ω

The Y matrix is shown and we will explain in details how is this obtained. Notice that this matrix has 4 rows and 4 columns, the same as the number of independent nodes in the circuit.

4 Ω 1 1 Ω 2 j1 Ω 3 4 3 Ω j0.25 ℧ 2 Ω -j2 Ω j3 Ω
1 -1 0 0
-1 (1 + 0.5 + 0.33 + 0.25 - j1) -(0.33 - j1) -(0.25)
0 -(0.33 - j1) (0.33 - j1 + j0.25 + j0.5) -(j0.25)
0 -(0.25) -(j0.25) (0.25 + j0.25 - j0.33)
0.25 ℧ 1 1 ℧ 2 -j1 ℧ 3 4 0.33 ℧ j0.25 ℧ 0.5 ℧ j0.5 ℧ -j0.33 ℧

The diagonal elements of this matrix is the sum of the admittances connected to the corresponding node. For example, (1 + 0.5 + .33 + 0.25 - j1)

1 -1 0 0
-1 (1 + 0.5 + 0.33 + 0.25 - j1) -(0.33 - j1) -(0.25)
0 -(0.33 - j1) (0.33 - j1 + j0.25 + j0.5) -(j0.25)
0 -(0.25) -(j0.25) (0.25 + j0.25 - j0.33)
0.25 ℧ 1 1 ℧ 2 -j1 ℧ 3 4 0.33 ℧ j0.25 ℧ 0.5 ℧ j0.5 ℧ -j0.33 ℧

Let’s go through each element together to show how the Y-matrix is obtained.

1 -1 0 0
-1 (1 + 0.5 + 0.33 + 0.25 - j1) -(0.33 - j1) -(0.25)
0 -(0.33 - j1) (0.33 - j1 + j0.25 + j0.5) -(j0.25)
0 -(0.25) -(j0.25) (0.25 + j0.25 - j0.33)
0.25 ℧ 1 1 ℧ 2 -j1 ℧ 3 4 0.33 ℧ j0.25 ℧ 0.5 ℧ j0.5 ℧ -j0.33 ℧

The diagonal elements of this Y matrix is the sum of the admittances connected to the corresponding node. There is only one admittance connected to node 1, and therefore, Y11
is 1 moh.

1 -1 0 0
-1 (1 + 0.5 + 0.33 + 0.25 - j1) -(0.33 - j1) -(0.25)
0 -(0.33 - j1) (0.33 - j1 + j0.25 + j0.5) -(j0.25)
0 -(0.25) -(j0.25) (0.25 + j0.25 - j0.33)
0.25 ℧ 1 1 ℧ 2 -j1 ℧ 3 4 0.33 ℧ j0.25 ℧ 0.5 ℧ j0.5 ℧ -j0.33 ℧

The off-diagonal elements are the negative of the admittances between the corresponding nodes. Between nodes 1 and 2, there is one admittance of 1 mohs, therefore, Y12 is -1 as shown.

1 -1 0 0
-1 (1 + 0.5 + 0.33 + 0.25 - j1) -(0.33 - j1) -(0.25)
0 -(0.33 - j1) (0.33 - j1 + j0.25 + j0.5) -(j0.25)
0 -(0.25) -(j0.25) (0.25 + j0.25 - j0.33)
  ℧ 1    ℧ 2    ℧ 3 4    ℧     ℧     ℧     ℧     ℧

There is no direct link between nodes 1 and 3 and, therefore Y13 is 0.

1 -1 0 0
-1 (1 + 0.5 + 0.33 + 0.25 - j1) -(0.33 - j1) -(0.25)
0 -(0.33 - j1) (0.33 - j1 + j0.25 + j0.5) -(j0.25)
0 -(0.25) -(j0.25) (0.25 + j0.25 - j0.33)
  ℧ 1    ℧ 2    ℧ 3 4    ℧     ℧     ℧     ℧     ℧

Similarly, Y14 is 0.

1 -1 0 0
-1 (1 + 0.5 + 0.33 + 0.25 - j1) -(0.33 - j1) -(0.25)
0 -(0.33 - j1) (0.33 - j1 + j0.25 + j0.5) -(j0.25)
0 -(0.25) -(j0.25) (0.25 + j0.25 - j0.33)
0.25 ℧ 1 1 ℧ 2 -j1 ℧ 3 4 0.33 ℧ j0.25 ℧ 0.5 ℧ j0.5 ℧ -j0.33 ℧

Note that the matrix is symmetric because the admittance between nodes k and m is the same as the admittance between nodes m and k. Therefore Y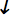21 is the same as Y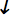12

1 -1 0 0
-1 (1 + 0.5 + 0.33 + 0.25 - j1) -(0.33 - j1) -(0.25)
0 -(0.33 - j1) (0.33 - j1 + j0.25 + j0.5) -(j0.25)
0 -(0.25) -(j0.25) (0.25 + j0.25 - j0.33)
0.25 ℧ 1 1 ℧ 2 -j1 ℧ 3 4 0.33 ℧ j0.25 ℧ 0.5 ℧ j0.5 ℧ -j0.33 ℧

To find Y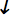22, add the admittances connected to node 2, these are:1 + 0.5 + 0.33 + 0.25 -j1, therefore, Y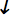22 is 2.08 -j1, which is the sum of the admittance connected to node 2.

1 -1 0 0
-1 (1 + 0.5 + 0.33 + 0.25 - j1) -(0.33 - j1) -(0.25)
0 -(0.33 - j1) (0.33 - j1 + j0.25 + j0.5) -(j0.25)
0 -(0.25) -(j0.25) (0.25 + j0.25 - j0.33)
0.25 ℧ 1 1 ℧ 2 -j1 ℧ 3 4 0.33 ℧ j0.25 ℧ 0.5 ℧ j0.5 ℧ -j0.33 ℧

There are two admittances between nodes 2 and 3, and therefore, Y23 is equal to the negative of (0.33 - j1)

1 -1 0 0
-1 (1 + 0.5 + 0.33 + 0.25 - j1) -(0.33 - j1) -(0.25)
0 -(0.33 - j1) (0.33 - j1 + j0.25 + j0.5) -(j0.25)
0 -(0.25) -(j0.25) (0.25 + j0.25 - j0.33)
0.25 ℧ 1 1 ℧ 2 -j1 ℧ 3 4 0.33 ℧ j0.25 ℧ 0.5 ℧ j0.5 ℧ -j0.33 ℧

The admittance connected to nodes 2 and 4 is -(0.25).

1 -1 0 0
-1 (1 + 0.5 + 0.33 + 0.25 - j1) -(0.33 - j1) -(0.25)
0 -(0.33 - j1) (0.33 - j1 + j0.25 + j0.5) -(j0.25)
0 -(0.25) -(j0.25) (0.25 + j0.25 - j0.33)
  ℧ 1    ℧ 2    ℧ 3 4    ℧     ℧     ℧     ℧     ℧

Again, we find no direct link between nodes 3 and 1 and, therefore, Y31 is 0.

1 -1 0 0
-1 (1 + 0.5 + 0.33 + 0.25 - j1) -(0.33 - j1) -(0.25)
0 -(0.33 - j1) (0.33 - j1 + j0.25 + j0.5) -(j0.25)
0 -(0.25) -(j0.25) (0.25 + j0.25 - j0.33)
0.25 ℧ 1 1 ℧ 2 -j1 ℧ 3 4 0.33 ℧ j0.25 ℧ 0.5 ℧ j0.5 ℧ -j0.33 ℧

There are two admittances between nodes 2 and 3, and therefore, Y32 is equal to the negative of (0.33 - j1).

1 -1 0 0
-1 (1 + 0.5 + 0.33 + 0.25 - j1) -(0.33 - j1) -(0.25)
0 -(0.33 - j1) (0.33 - j1 + j0.25 + j0.5) -(j0.25)
0 -(0.25) -(j0.25) (0.25 + j0.25 - j0.33)
0.25 ℧ 1 1 ℧ 2 -j1 ℧ 3 4 0.33 ℧ j0.25 ℧ 0.5 ℧ j0.5 ℧ -j0.33 ℧

There are 4 admittances connected to node Y33; 0.33, -j1, j0.25, and j0.5.

1 -1 0 0
-1 (1 + 0.5 + 0.33 + 0.25 - j1) -(0.33 - j1) -(0.25)
0 -(0.33 - j1) (0.33 - j1 + j0.25 + j0.5) -(j0.25)
0 -(0.25) -(j0.25) (0.25 + j0.25 - j0.33)
  ℧ 1    ℧ 2    ℧ 3 4    ℧     ℧     ℧     ℧     ℧

Continuing with this procedure, the following Y-matrix is obtained:

1 -1 0 0
-1 (1 + 0.5 + 0.33 + 0.25 - j1) -(0.33 - j1) -(0.25)
0 -(0.33 - j1) (0.33 - j1 + j0.25 + j0.5) -(j0.25)
0 -(0.25) -(j0.25) (0.25 + j0.25 - j0.33)